Common Transversals and Tangents
Frank SottileUniversity of Masssachusetts, Amherst
Symbolic Computational Algebra 2002
University of Western Ontario

Common Transversals and TangentsFrank SottileUniversity of Masssachusetts, Amherst Symbolic Computational Algebra 2002 University of Western Ontario |

|
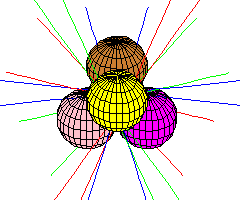
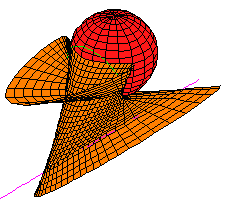
We describe some interesting symbolic computations that arose while studying the following simple geometric problem:
Consider k lines and 4-k spheres in R3.
Besides the interesting geometry, computation, and pictures, we feel that the
study of geometry in 3-space is a fertile area for potential applications of
symbolic and computational algebra.
The results in this talk represent joint work with
Gabor Megyesi and
Thorsten Theobald.
A
web page
featuring many, many pictures from this study.