CANARIE E-content Program

CA: Monet

Mathematics On the NET

Final Report

1.0 Description of Project

The project CA: Monet funded a Canadian partner (UWO/ORCCA) to participate in, and benefit from, a major European ESPRIT Information Society Technologies (IST) project to develop tools and technologies for Mathematics on the Web (IST-2001-34145). The joint Canadian-European project “Mathematics on the NET” (Monet) was undertaken by the Monet Consortium, which included several collaborators from Universities and companies in Europe and the University of Western Ontario, as its Canadian partner.

The global project intended to design tools and protocols capable of capturing the semantics of mathematical E-content and of providing a rich environment in which mathematical content can be used interactively. These tools are to be used directly by people, to explore, search or solve problems, or be used by software agents to support services, with protocols to allow the necessary service description and discovery. In this framework, a user’s query is typically a semantically rich expression of the mathematical objects with which they are working and the problem they wish to solve, plus constraints on the method of solution and other mathematical objects involved. Every mathematical service describes itself in terms of the problems it is designed to handle, how it handles them, (e.g. look up the answer in a database, use a particular algorithm or launch a appropriate mathematical software package), and who is allowed to access it. Services advertise their presence when they start up by contacting one or more brokers whose job it is to match a user’s query to the capabilities of the available services. Brokers may exchange information about available services with each other so that requests that cannot be handled locally can be passed on to a more remote service. Matching queries to services is non-trivial since it often involves making qualitative decisions on the basis of mathematical domain-specific knowledge. Since the brokers are not intended to have much, if any, mathematical capability themselves, they need to choose a solution service or recommend a solution strategy from a problem description.

The aim of the global Monet project was to demonstrate that this structure is both feasible and practical. As was anticipated at the beginning of the project, the Monet Consortium has achieved the following objectives: (1) identified key technologies for deploying and using mathematical content and services, (2) developed a mechanism for describing queries and a mathematical service description language, (3) constructed at least one broker that can match services to queries, along with other necessary content infrastructure, (4) constructed over 20 services for problem solving, including both numerical and symbolic.

The present project developed the base technologies for a framework to allow distributed online collaboration between individuals and among agents, and share common languages for describing mathematical content and capabilities. The potentially affected demographics are significant, comprising education at the secondary and post-secondary levels as well as all areas of technical collaboration. These technologies are inextricably tied to broadband networks as collaborations and services in this area naturally span geographic distances.

A large part of the effort in this project was devoted to developing suitable ontological tools, that is, tools to create, manipulate and use domain knowledge frameworks for mathematics. This was supposed to enable rich content and meaningful service description and discovery for mathematical E-content. A second significant effort was in developing of proof-of-concept prototypes for mathematical services to operate on mathematical E-content.

ORCCA at the university of Western Ontario undertook the following concrete objectives:

o Develop the necessary specification vocabulary to formulate a set of problems for specific mathematical services, e.g. solving systems of equations, symbolic integration and symbolic differentiation. These are in form of OpenMath content dictionaries, Mathematical Service Description Languages and WSDL.

o To design and create general tools for the creation of mathematical web services.

o To use these tools to develop prototype servers based on Maple for specific mathematical web services.

The project is innovative throughout: key aspects of describing services mathematically, based on systematized knowledge bases (ontologies); the technology to build these ontologies; the publication, discovery and composition of services based on these descriptions; and the exchange of mathematical objects in XML representations.

2.0 Project Results

· Overview of project work and results.

The Monet project has succeeded in enhancing the semantic web on-line media capacities to use mathematical content in a first-class manner, and in a way that can be customized both to educational level and cultural preferences. It can express problems and queries using semantically rich mathematical objects and provide services to solve them.

The global Monet project has demonstrated the feasibility of the broker-based framework architecture (as shown in the Figure 1) to enable an optimal web communication between mathematical software and users. The latest available Semantic Web technologies are used to discover semantically rich mathematical objects, to provide and advertise mathematical web services.

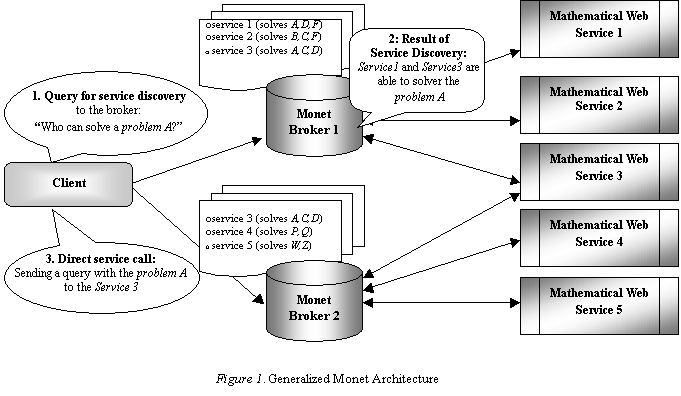
As stated in the Final Review Report for the global Monet project, “.. the web technologies delivered – compatible with the state-of-art – can even provide a useful contribution e.g. to the development of the computational gird and become an important tool for software engineering. The tools can be modified without bigger efforts to be extended to a web services.”

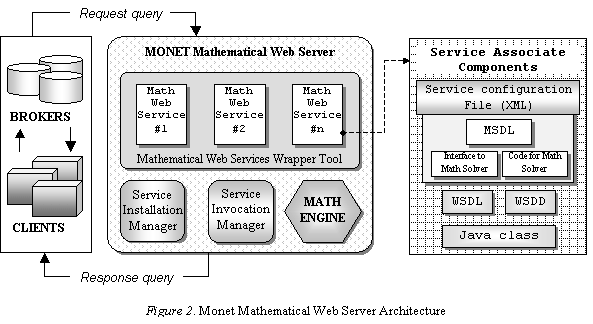
The Canadian Monet project succeeded in developing an application framework for providing mathematical web services, and populating it with a number of demonstrator services. The framework has tested the approach of using a single wrapper service around a computer algebra system and configuring that service via an XML specification of the mathematical service (as shown in the Figure 2). The XML configuration file includes all elements to publish the service via MSDL and to configure the algebra system to provide the service. This approach contrasts with the approach taken at the Numerical Algorithm Group, where new Java code must be written for each service. Trying both approaches was a valuable experience and provides convincing evidence for the direction we have taken.

At the end of the project we experimented with an open-ended Maple to OpenMath converter (i.e. the block used to convert mathematical results back from the server’s representation to the network, vendor-neutral representation). This is a tantalizing direction because OpenMath is inherently extensible, and it would be highly desirable to be able to convert any combination of user-defined mathematical objects. This remains a promising direction for future work.

The project results allow both service providers and clients to benefit from the Monet architecture: Clients do not have to have all necessary mathematical software installed locally, and are not required to know the syntax and calling sequences of multiple mathematical software packages. Service providers can expose their latest, sophisticated mathematical software to a larger target audience, reduce maintenance costs for old versions, and potentially derive transaction-based revenue.

The implementation of portable Symbolic Web Server and its Mathematical Service Wrapper allows to install a new symbolic solving facility by a university professor or a developer of computer algebra package, because it assumes no special knowledge about the specifics of this architecture. For example, experts in symbolic computation, proficient in Maple, were able to develop a set of Maple packages solving specific problems such as Symbolic and Fractional Differentiation, Approximate GCD for polynomials and then used the Symbolic Web Server to create mathematical web services to make solvers for those problems available on the framework.

The set of ontologies and languages developed within MONET project provided a platform-neutral way of representation of mathematics. This result us used for mathematical knowledge management in such areas as mathematical problem description and unification of different mathematical formats. The last found an application in OpenMath - Maple conversion tools that allow Maple to import mathematical data and export results of computation in a uniform standard.

· Direct outcomes: specific deliverables as identified in SoW.

Expected deliverables:

• D15: Symbolic Services. Beta Version,
• D21: Symbolic Services Release Candidate,
• D23: Wrapper Tool Release Candidate,
• D30: Other Demonstrator Applications.

Actual outcomes:

• D15 complete: Symbolic Services architecture proposed and first test Symbolic services launched.
• D21 complete: Enhanced the architecture designed in D15 and validated the approach developed. Extended the problem area covered by test symbolic services.
• D23 complete: Wrapped the final implementation of Symbolic Solver architecture to be used with other solver engines, such as computer algebra systems or theorem provers.
• D30 complete: Developed over 7 various applications able to be exposed as Monet services by using auxiliary adapter and/or wrapping software

2.1 E-content Program Objectives

We strongly believe the Monet project meets the CANARIE program objectives in all of it aspects. The principal objective of the Monet project was to develop advanced prototypes of key technologies that can be used to deploy and interact with services for mathematical E-content on the world-wide web, and to demonstrate their effectiveness in practice. These were achieved by developing a number of ontologies, languages and protocols, used in communication between components of the Monet architecture. The languages and protocols were developed, based on the widely used content representation standards of MathML and OpenMath.

Secondly, we developed a number of technologies to create and maintain a problem solving environment based on a framework for distributed mathematical web services. Our approach allows clients to access these web services through a uniform set of network protocols, independent of the software packages that provide the end functionality.

2.2 Phase Deliverables

Objective/Deliverable	Actual Achievement with Comments
D15: Symbolic Service Initial Beta Version (intermediate milestone).	This deliverable provides a number of web services for a limited set of symbolic functionalities including integration, differentiation and root finding for univariate equations. The software delivered for D15 implements a prototype of a symbolic solver environment. It includes Java packages for mathematical service tools, a mathematical broker prototype and a basic client interface. The software also contains a kit of shell scripts to maintain the mathematical service environment. Maple code for the symbolic services provided was also submitted with the deliverable.
D08: Broker Initial Beta Version (additional deliverable - added during the project)	This deliverable offers an implementation of the prototype for a mathematical broker, originally developed as scaffolding while our partners developed a sophisticated broker. This naïve broker served as the basic broker for the international project right up to the last quarter.
D21: Symbolic Service Release Candidate	This deliverable provides a number of web services for an extended set of functionality. The deliverable software provides 7 symbolic services, such as can solve systems of polynomial equations, compute limits and expand functions in series. Core software for those services consists of Maple code implementing their functionality and Java tools for their generation. Software assigned to D21 also includes specially designed Maple packages to drive direct conversion between OpenMath and Maple formats within Maple computer algebra system. The software delivered contains a Java package implementing a universal graphical interface for clients of symbolic services. D21 is an intermediate milestone.
D23: Wrapper Tools Release Candidate	This deliverable offers technologies and software tools that allow programmers to create new symbolic services based on various computer algebra systems, such as Maple and Axiom. These software tools provide the full symbolic service functionality and demonstrate the applicability of the ontologies, protocols and frameworks developed in other project work packages. The software tool kit is prepared to perform smooth integration with other functional parts of the Monet architecture such as the Registry Manager and the Execution Manager. The web-based interface for the symbolic service client is designed to ease access to symbolic services developed. A software package to generate web-interface client pages corresponding to Monet services was also included in the deliverable.
D30: Other Demonstrator Applications	This deliverable demonstrates other symbolic applications, not necessary designed within Monet project architecture, but still able to be exposed as Monet services by using some adapter and/or wrapping software. The following software was developed within this deliverable: · Mathematical format conversion, including conversion between following mathematical formats: presentation MathML, LaTeX, Maple, Content MathML, OpenMath (partly developed using web servlets and as JavaServer pages technologies); · QRGCD (computation of the greatest common divisor of approximate polynomials); · Symbolic order differentiation (developed as a MONET symbolic service); · Fractional order differentiation (developed as a MONET symbolic service). The following software is available on-line: 1. Web Client for Monet Symbolic Services http://ptibonum.scl.csd.uwo.ca:16661/MonetServiceClient/ 2. MathML – LaTeX translator: http://www.orcca.on.ca/MathML/texmml/textomml.html 3. Content MathML to Presentation MathML (stylesheets) http://www.orcca.on.ca/MathML/software/mmlctop2_0.xsl 4. Mathematical notation selection tool http://ptibonum.scl.csd.uwo.ca:16661/NotationSelectionTool/

2.3 Overall Objectives

Rating _10_

To illustrate that project met its objectives one may review the concrete objective stated in the Project Agreement. In the table below we indicate the status of achieving tasks in each objective and corresponding deliverables.

Objective	Status
o Develop the necessary specification vocabulary to formulate a set of problems for specific mathematical services, e.g. solving systems of equations, symbolic integration and symbolic differentiation. These will be in form of OpenMath content dictionaries, Mathematical Service Description Languages and WSDL.	Complete in deliverables D15: Symbolic Service Initial Beta Version and D21: Symbolic Service Release Candidate
o To design and create general tools for the creation of mathematical web services.	Complete in deliverable D23: Wrapper Tools Release Candidate
o To use these tools to develop prototype servers based on Maple for specific mathematical web services.	Complete in deliverables D23: Wrapper Tools Release Candidate and D30: Other Demonstrator Applications.

2.4 Project Contribution to Sector/Social Objectives

Rating __8__

This project has had a significant impact on the way that mathematical content and services can participate in the semantic web. Mathematics is nothing but another language, used to express ideas precisely in all manner of technical areas. We see this project addressing the major structural barriers that impede the use of mathematical E-content. Given the widespread reliance of mathematics in most technical areas, not just education, this work has impact on to all technical broadband services.

Before the advent of the OpenMath and MathML standards, mathematical E-content was captured solely graphically, with pictures of formulas. This meant that mathematical E-content was not meaningfully accessible to network tools, could not be searched or transformed, and could not be used in web services. The problem is that, in a semantically rich web, pictures of equations are insufficient to allow any meaningful operations. In the words of Magritte, "Ceci n’est pas une pipe." (The painting was only a picture of a pipe.)

The sector goal of this project has been to bring mathematical E-content to the fore as a first-class participant in data exchange, knowledge management and web services. We have met or superseded all of our stated objectives in this direction.

3.0 Schedule

Objective/Deliverable	Original Completion Date (SOW)	Actual Finishing Date	Final Status of Task/ Deliverable
D15: Symbolic Service Initial Beta Version (intermediate milestone).	August 2003	August 2003	complete
D21: Symbolic Service Release Candidate	November 2003	December 2003	complete
D23: Wrapper Tools Release Candidate	December 2003	February 2004	complete
D30: Other Demonstrator Applications	March 2003	March 2004	complete

The main reason for the delay with the deliverable “D21: Symbolic Service Release Candidate” was due to extra efforts that the University of Western Ontario has put into developing of the Mathematical Broker Prototype (Deliverable D08: Broker Initial Beta Version). While our collaborators were developing a fully functional sophisticated broker we needed to have its “placeholder” to verify the client/broker/server architecture.

The main reason for the delay with the deliverable “D23: Wrapper Tools Release Candidate” was due to our decision to develop a set of experimental mathematical formats conversion tools, such as OpenMath-Maple converter. We believe such an addition to the project outcomes is able to significantly extend the area of potential application of the project results.

4.0 Profile of Project Participants

Organization Name	Province of Operation	Organization Type @	Industrial Sector*	Number of Employees*	Annual Expenditures*
The University of Western Ontario	Ontario	UN	Education	3 251	388,727,000

@ UN-university, GR-gov’t research laboratory, PPR-public/private sector research organization, PU – public sector, PR – private sector for private sector firms only

4.1 Profile of additional collaboration

Organization Name	Province of Operation	Organization Type @	Industrial Sector*	Nature of support
The Numerical Algorithms Group (NAG)	Oxford, UK	PPR	Software Technology	Coordinating Partner of European part of the project. Brought background technologies to the project. Developed new ontologies and numerical services. Participated in creation and testing of an integrated problem solving environment. NAG provided peer review and feedback on results achieved by the University of Western Ontario.

Le laboratoire I3S (Informatique, Signaux et Systèmes de Sophia-Antipolis)	Sophia Antipolis, France	GR	Engineering technologies	Brought background technology to the project. Participated in development of new technology for Monet Mathematical Broker (Registry Manager). Participated in creation and testing of an integrated problem solving environment. Organized and hosted one project meeting, provided peer review and feedback on results achieved by the University of Western Ontario.
The Technische Universiteit Eindhoven (TU/e)	Eindhoven, the Netherlands	UN	Education	Brought background technology to the project. Participated in development of new technology for Monet Mathematical Broker (Planning Manager). Participated in creation and testing of an integrated problem solving environment. Organized and hosted one project meeting, provided peer review and feedback on results achieved by the University of Western Ontario.
The Victoria University of Manchester	Manchester, UK	UN	Education	Brought background technology to the project. Participated in development of new technology for Monet Mathematical Broker (Instance Store). Participated in creation and testing of an integrated problem solving environment. Organized and hosted one project meeting, provided peer review and feedback on results achieved by the University of Western Ontario.
Stilo Ltd	Bristol, UK	PPR	Software Technology	Brought background technology to the project. Participated in development of new technology for Monet Mathematical Broker (Execution Manager). Participated in creation and testing of an integrated problem solving environment. Organized and hosted one project meeting, provided peer review and feedback on results achieved by the University of Western Ontario.
The University of Bath	Bath, UK	UN	Education	Brought background technology to the project. Participated in development of an alternative technology for Symbolic Services. Trying both approaches developed by Bath and by UWO was a valuable experience and provided convincing evidence for direction we have taken. University of Bath organized and hosted a project meeting, provided peer review and feedback on results achieved by the University of Western Ontario.
The University of Nice-Sophia Antipolis	Nice and Sophia Antipolis, France	UN	Education	Brought background technology to the project. Participated in development of new technology for Monet Mathematical Broker. Participated in creation and testing of an integrated problem solving environment.

5.0 Project Participation

5.1

Organization Name	Participate in R&D	Involved in testing/pilot	Commercialization	Other (please describe)
The University of Western Ontario	x	x	x
The Numerical Algorithms Group (NAG)	x	x	x
Le laboratoire I3S	x	x	-
The Technische Universiteit Eindhoven (TU/e)	x	x	-
The Victoria University of Manchester	x	x	-
Stilo Ltd.	x	x	x
The University of Bath	x	x	-
The University of Nice-Sophia Antipolis	x	x	-

5.2

Organization Name	Contribution as proposed	Increased Contribution	Reduced contribution	No Contribution	Joined after project began
The University of Western Ontario		OpenMath-Maple converter, Math Broker prototype	-	-	-

6.0 Project Budget and Funding

Project Funding	Levels in Project Agreement	Percentage of Total	Actual levels	Percentage of Total
CANARIE funding
Other federal funding
Other public funding		C O N F I D E N T I A L
Participants’ Eligible Contributions
Total

Project Budget

Cost Categories	SoW Budget	Actual Eligible Cost	Variance*	Reasons
Labour **
Consultants – Sub-contractors
Direct Materials
Travel and Training		C O N F I D E N T I A L
Travel
Other
Special Purpose Equipment
Project Total

* ($) under-budget, $0 on- budget, $ over- budget
** Direct Labour includes Overhead and Fringe Benefits

Special Purpose Equipment	SoW Budget	Actual Cost	Residual Value	Recipient
	C O N F I D E N T I A L
SPE Total

7.0 Budget Allocation

Participant	CANARIE	Other federal	Other Public	Participant Eligible Contributions
Lead Contractor
-		C O N F I D E N T I A L
-
Total

8.0 Additional Contributions

Participant	Capital Equipment	Software	Other	Dollar value
Lead Contractor		Mathematical Broker Prototype		No residual value (needed for project development)

9.0 Information Dissemination/Technology Transfer

9.1 Conferences/Workshops

Conference/ Workshop/Seminar	Category	Registration Fee (y/n)	Number attending	Audience
Ontario Research Centre for Computer Algebra, joint laboratory meetings (once a month)	OT sponsored by Ontario Research Centre for Computer Algebra (ORCCA)	n	50	Faculty and students of Canadian, French, Austrian and American Universities, as well as people from and private software engineering companies.
Applications for Computer Algebra (ACA) 2003. Raleigh, NC, July 2003.	OT	y	300	Researchers and software developers in the area of computer algebra.
International Symposium on Symbolic and Algebraic Computation (ISSAC), Philadelphia, PA, August 2003, Philadelphia	OT sponsored by Association for Computing Machinery (ACM)	y	500	Researchers and software developers in the area of computer algebra and symbolic computation.
Calculemus 2003, 11th Symposium on the Integration of Symbolic Computation and Mechanized Reasoning, Rome, Italy, September 2003	OT sponsored by the European Network of Excellency in Computational Logic	y	200	Researchers in the common domains of symbolic computation and automatic theorem proving.
MONET (Mathematics On The NET) Workshop, University of Bristol, UK,	OT sponsored by Information Society Technologies (IST)	n	20	People involved in the Monet Consortium
Mathematical Knowledge Management (MKM) conference, Phoenix AZ, January 2004	OT sponsored by - American Mathematical Society (AMS) - Mathematical Association of America (MAA) and al.	n	50	Researchers and software developers in the area of Mathematical Knowledge Representation and Management
Mathematics On the NET, Nice, France	OT sponsored by Information Society Technologies (IST)	n	20	People involved in the Monet Consortium
University of Western Ontario Research in Computer Science (UWORCS) 2004, March 2, 2004	OW sponsored by the university of Western Ontario, dept. of Computer Science	n	100	Faculty and students of Canadian Universities
Mathematics On the NET, Bath UK, March 2004	OT sponsored by Information Society Technologies (IST)	n	20	People involved in the Monet Consortium
Mathematics of Computer Algebra and Analysis, (MOCAA), University of Waterloo, Waterloo ON, Canada, May 2004	OT sponsored by - Fields Institute - Mathematics of Information Technology and Complex Systems ( MITACS )	n	200	Researchers and software developers in the area of computer algebra and numerical analysis.
East Coast Computer Algebra Day 2004 (ECCAD), Wilfrid Laurier University, Waterloo ON, Canada, May 2004	OT sponsored by - Faculty of Science of the Wilfrid Laurier University, - Waterloo Maple, Maplesoft Inc, - National Science Foundation (NSF), - Natural Sciences and Engineering Research Council (NSERC) - Mathematics of Information Technology and Complex systems, (MITACS), - TechnicalMastery.com Corporation, - Ontario Research Centre for Computer Algebra (ORCCA)	n	200	Researchers and software developers in the area of computer algebra.
OpenMath Meeting, Helsinki, Finland, May 2004	OT sponsored by - OpenMath Thematic Network - the Department of Mathematics and Statistics, University of Helsinki	n	100	Researchers from Universities and private companies, involved in developing OpenMath standard.
International Symposium on Symbolic and Algebraic Computation (ISSAC), Spain, July 2004.	OT sponsored by - Research Institute for Symbolic Computation (RISC), - Johann Radon Institute for Computational and Applied Mathematics (RICAM), - Association for Computing Machinery (ACM), - Fundación Caja Cantabria, - University of Cantabria - Maplesoft Inc.	y	500	Researchers and software developers in the area of computer algebra and symbolic computation.
Internet Accessible Mathematical Computation a Workshop at ISSAC 2004, University of Cantabria, Santander, Spain, July 2004.	OT sponsored by - the Ministry of Education of Cantabria - Natural Sciences and Engineering Research Council (NSERC)	n		Researchers and software developers in the area of distributed mathematical computation accessible via the Internet.
The 10th International Conference on Applications of Computer Algebra (ACA 2004), Beaumont, Texas, USA, July 2004	OT sponsored by - National Science Foundation (NSF) - Lamar University, - International Association for Mathematics and Computers in Simulation (IMACS)	y		Researchers and software interested in serious applications of symbolic computation theories and tools for mathematics, logic, science, engineering and education.
Seminar at the University of Limerick, Ireland, August 2004,	OT sponsored by the University of Limerick	n		Faculty and students of the Computer Science Department of the University of Limerick
Mathematical Knowledge Management, Third International Conference, MKM, September 2004	OT sponsored by - Centrum Informatyki "ZETO" S.A, - Minister of Scientific Research and Information Technology of Poland, - "Andrzej Malec i Wspólnicy", - BOS S.A.	y		Researchers and software developers in the area of Mathematical Knowledge Representation and Communication

9.2 Publications

Article title and location	Audience
1. Clare M. So, Elena Smirnova, Stephen M. Watt. An Architecture for Distributed Mathematical Web Services, in: Andrea Asperti, Grzegorz Bancerek, Andrzej Trybulec (Eds.): Mathematical Knowledge Management, Third International Conference, MKM 2004/LNCS 3119 Springer-Verlag, 2004. pages 363-377	Researchers and software developers in the area of Mathematical Knowledge Representation and Communication
2. Elena Smirnova, Stephen M. Watt. Symbolic Solver Services. Wrapper Tools Release Candidate. Technical Report for MONET Project: Public Deliverable 23, The MONET Consortium (IST-2001-34145), 2004, 61 pages.	Researchers and software developers in the area of Mathematical Communication
3. Walter Barbera-Medina, Elena Smirnova, Clare M. So and Stephen M. Watt. Symbolic Service Release Candidate. Technical Report for MONET Project: Public Deliverable 21, The MONET Consortium (IST-2001-34145), 2004, 35 pages.	Researchers and software developers in the area of Mathematical Communication
4. E. Smirnova, S.M. Watt. Using Computer Algebra Systems In The Development of Mathematical Web Services, East Coast Computer Algebra Day 2004 (ECCAD), May 2004, Wilfrid Laurier University, Waterloo ON, Canada, http://www.cargo.wlu.ca/e-ECCAD2004/main.pdf, page 12.	Researchers and software developers in the area of computer algebra and its applications
5. E. Smirnova, Clare M. So, S.M. Watt. Providing mathematical Web Services Using Maple in the MONET Architecture, MONET Workshop University of Bath, 16-17 March 2004, http://monet.nag.co.uk/cocoon/monet/proceedings/MONET-UWO.pdf	Researchers and software developers in the area of Frameworks for Mathematical Web services
6. E. Smirnova, S.M. Watt. An Approach to Mathematical Notation Selection, Abstract of paper for the Second North American Workshop on Mathematical Knowledge Management, Phoenix, Arizona, 2004, http://imps.mcmaster.ca/na-mkm-2004/abstracts/smirnova-watt.pdf	Researchers and software developers in the area of mathematical knowledge representation and mathematical data communication
7. Robert M. Corless, Stephen M. Watt and Lihong Zhi. QR Factoring to Compute the GCD of Univariate Approximate Polynomials, IEEE Transactions on Signal Processing, Vol. 52, No. 12, pp. 3394-3402, December 2004.	Researchers and software developers in the area of area of numeric and symbolic and computation.
8. W.A. Naylor and S.M. Watt. Meta-Stylesheets for the Conversion of Mathematical Documents into Multiple Forms, Annals of Mathematics and Artificial Intelligence, Vol. 38, pp. 3-25, 2003	Researchers and software developers in the area of mathematical data formats and representation.
9. S.M. Watt. MathML, in Handbook of Computer Algebra J. Grabmeier, E. Kaltofen, V. Weispfenning (editors) , Springer Verlag, Heidelberg 2003 ISBN 3-540-65466-6, , pp. 154-160	Anyone who uses MathML as a mean to encode mathematics on the web.
10. S.M. Watt, Optimizing Compilation for Symbolic-Numeric Computing, pp. 18-, Proc. 6th International Symposium on Symbolic and Numeric Algorithms for Scientific Computation (SYNASC 2004), September 26-30 2004, Timişoara Romania, MITRON Press ISBN 973-661-441-7.	Researchers and software developers in the area of symbolic and numeric computing
11. Mhenni M. Benghorbal and Robert~M.~Corless, Power series solutions of Fractional Differential Equations, International Journal of Pure and Applied Mathematics, 2004	Researchers in the area of symbolic computation
12. Mhenni M. Benghorbal and Robert~M.~Corless, A unified formula for arbitrary order symbolic derivatives and integrals of a rational polynomial, International Journal of Pure and Applied Mathematics, 2004	Researchers in the area of computer algebra and its applications

9.3 Print and Electronic Media (Promotion/Communication)

Title/event

Audience

10.0 Project Final Status

Project Final Status	Print X if true
Project cancelled before completion
Project incomplete
Proof of concept completed	X
Developed regulations, standards	X
Technology development not yet completed (no agreement on further work)
Technology development not yet completed (work continuing)
Technology development completed	X
Product/service development not yet completed (no agreement on further work)
Product/service development not yet completed (work continuing)
Product/service agreement completed	X
Other (please describe)

11.0 Application/Commercialization

Project Commercialization/Application Status	Print X if true
No plans to apply project results
Potential utilization of project results within partner organization(s) being studied
Project results being utilized within partner organization(s)	X
Project results commercialization on hold pending review/market study	X
Commercialization on hold pending search for partners
Commercialization in progress by project participants
Commercialization in progress with new partners
Application on hold pending search for partners
Application in progress by project participants	X
Application in progress with new partners (in our case not-for-profit)	X
Product/technology licensed
IP/Product/Methodology made available as open source.
IP/Product/Methodology planned to be available as open source.
Other (please describe)

12.0 Use of the Internet

The Internet played two essential roles in this project: 

First as a medium of collaboration for the project itself, the Internet was used to share intermediate project results as they were developed, and to test interacting software components between the project sites.

Secondly, the Internet is the primary target for the technologies developed in the project.

This role is central, since the principal objective of the project was to develop advanced prototypes of technologies that can be used to deploy and interact with services for mathematical E-content on the world-wide web.  (The possibility of private network deployment follows naturally from this.) Furthermore, the technologies developed within the project are closely tied to broadband networks as collaborations and services in this area naturally span geographic distances.

Most applications developed in the Monet project serve as prototypes and demonstrators for technologies designed.  Most of these prototype applications have been designed to be viable using presently available commercial Internet speeds. However, fully capable sophisticated Monet services in the future may transfer significant amounts of data between components of the architecture: clients, brokers and services. These will rely on higher capacity broadband networks. There are no inhibitors to using high bandwidth/speed for the architecture developed in this project.

13.0 Socio-economic Impacts

Beneficiaries

The potential beneficiaries of the project comprise (1) students and educators at the secondary and post-secondary levels, (2) workers in all areas of technical collaboration. In the year 2000, the total number of university undergraduate students in North America was 15.5 million. Of these 3.2 million were enrolled in a mathematics or statistics course (numbers courtesy of Maplesoft). If we estimate the Canadian portion to be 10% of this number, we see 300,000 university students as potential beneficiaries of improved mathematical E-content and services. This population spans levels of mathematical sophistication, mathematical culture and mother tongue. Meaningful treatment of mathematical E-content is required to deploy it to the target audience. The need to tailor mathematical notation and treatment is even greater at the secondary level, where the target audience is correspondingly larger. Beyond education, this work has potential impact on all technical professionals using mathematics in Canada. We do not have a ready estimate of this population size.

Intended Impacts

The principal benefit to the beneficiaries identified is to open the path to web services that deal with mathematical subject material as freely as current services deal with text and pricing. This includes, e.g., services to perform numerical and algebraic computations, to search mathematical materials, to provide technical training and evaluation, and to provide audit trails of engineering decisions.

Actual Impacts

The vision of the potential benefits of this project are broad and far-reaching. With this scope, it is too early to expect direct results to the end-beneficiaries. However, the work of the project is having an impact on the development strategy for mathematical software developers, including the Canadian company Maplesoft.

Contribution to Technical Research, Organizational and Cultural Innovation

Understanding the long-term nature of this work, as emphasized above, it is important to note that the present work has been quite important in forming the strategic scientific direction of the Ontario Research Centre for Computer Algebra. This is arguably one of the top handful of laboratories in the world working in the area of symbolic mathematical computation, and the software of its industrial partner, Maplesoft, is the leading symbolic math software used in education world-wide. Therefore, this effect on direction is far-reaching. More specifically, we see the role of mathematical web services for the evolving web as a model for self-organization of large, multi-component mathematical software of the future.

Follow-on Research and Development

University of Western Ontario looks forward to create and deploy a range of complex mathematical web services to create a fully functional problem solving environment for remote computation. Once a sufficient number of services are deployed, the Monet framework could be applied to a wide spectrum of applications, including professional technical services, mathematical education and distance learning, and research support in a number of domains. We intend to incorporate the MONET framework with the different facilities for mathematical education. The Atlantic Gateway for Math (AGATE-M) project, supported by the Centres for Research Into Science and Math Education is one of possible environments for such a collaboration.

14.0 Role of CANARIE

Please describe any benefits due to CANARIE’s role in this project.

Foremost, without CANARIE support we would not have been able to undertake this work, and would therefore not have been able to participate in the global working group.

Secondly, exposure to CANARIE’s E-content viewpoint helped us develop our views on how mathematics should participate in the larger E-content setting.

Please describe any problems caused by CANARIE’s role in this project.

The level of detail in budgeting resource allocation and expenditures (by person, by period, etc), and in reporting was overwhelmingly excessive. This level of effort would be appropriate for a project with budget of 10 times the size, but the level of granularity would even then have to be reduced.

Surely the amount of work involved in project preparation and reporting creates a corresponding analytical burden at CANARIE. The support of the CANRIE analysts, and Ern Bieman in particular, was exemplary. However it is clear that the detail level required by the project places a burden on CANARIE as well.

Based on your experience, what can CANARIE do to improve program delivery and support to projects?

Simplify reporting requirements.

Other than that, the support has been great.

15.0 Evaluation Report

The overall evaluation of the international Monet project has been best summarized in the covering letter to the Final Review Report "... the final results reported here are overall very satisfactory. In fact, I think these are the highest numerical average scores I have hitherto had the pleasure to communicate in any review report". 

We attach a copy of the full Final Review Report of the global Monet project. The report was produced by the European Commission (Information Society Technologies Programme) and signed by 2 project reviewers Massimo Marchiori, Bernd Wegner and the project officer Johan Hagman on the 10^th of October, 2004.